1. Introduction
To
resolve a business problem, we may need to use a number of data mining models
with different algorithms and different algorithm parameters. You should find
the best one and deploy it into production. For this purpose, we need to measure
a model’s accuracy, reliability, and usefulness.
Accuracy
determines how well an outcome from a model correlates with real data. The
standard methods to measure accuracy include lift charts, profit charts, and
classification matrices.
Reliability assesses
how well a data mining model performs on different datasets. This is often
achieved by using cross validation. With cross validation, we partition the
training dataset into many smaller sections. SSAS then creates multiple models
on the cross sections using one section at a time as test data and other
sections as training data, trains the models, and creates many different
accuracy measures across partitions. If the measures across different
partitions differ widely, the model is not robust on different training and
test set combinations.
Usefulness
measures how helpful the information gathered with data mining is. Usefulness
is typically measured through the perception of business users, using
questionnaires and similar means.
2. Measuring Accuracy
a. Lift Charts
A
lift chart is the most popular way to show the performance of predictive
models. Figure below shows a lift chart for the predictive models of the
predicted variable (Bike Buyer) for the value 1 (buyers).
The
chart shows four curved lines and two straight lines. The four curves show the
predictive models (Decision Trees, Naïve Bayes, Neural Network, and
Clustering), and the two straight lines represent the Ideal Model (top) and the
Random Guess (bottom). The x-axis represents the percentage of population (all
cases), and the y-axis represents the percentage of the target population (bike
buyers).
From
the Ideal Model line, you can see that approximately 48 percent of Adventure
Works customers buy bikes. That means that, IDEALLY, if you could predict with
100 percent probability which customers will buy a bike and which will not, you
would need to target only 48 percent of the population. On the other hand, the
Random Guess line indicates that if you were to pick cases out of the population
randomly, you would need 100 percent of the cases for 100 percent of bike
buyers. Likewise, with 80 percent of the population, you would get 80 percent
of all bike buyers, with 60 percent of the population 60 percent of bike
buyers, and so on.
Data
mining models give better results in terms of percentage of bike buyers than
the Random Guess line but worse results than the Ideal Model line. From the
lift chart, we can measure the lift of the data mining models from the Random
Guess line. For example, if you take the highest curve, directly below the
Ideal Model line, we can see that if we select 70 percent of the population
based on this model, you would get nearly 88 percent of bike buyers. From the
Mining Legend window, we can see that this is actually 87.49% for the Decision
Trees model.
The value for Predict
probability represents
the threshold required to include a customer among the "likely to
buy" cases. For example, to identify the customers from the decision tree
model who are likely buyers, we would use a query to retrieve cases with a
Predict probability of at least 32.54% (assuming we select 70
percent of the population). To get the customers
targeted by the last model – the clustering model, we would create query that
retrieved cases with a Predict
Probability value of at
least 41.50%.
It is interesting to compare the models. Still assuming we
select 70 percent of the population, the decision
tree model appears to capture more potential customers, but when you target
customers with a prediction probability score of 32.5%, we also have a 67.5%
chance of sending a mailing to someone who will not buy a bike. On the other
hand, the clustering model captures less potential customers, but we have a
less chance (58.5% = 1-41.5%) of sending a mailing to someone who will not buy
a bike. Therefore, if we were deciding which model is better, we would want to
balance the greater precision and smaller target size of the filtered model
against the selectiveness of the basic model. This is better addressed with the
Profit Chart discussed below.
The value for Score helps us compare models by calculating
the effectiveness of the model across a normalized population. A higher score
is better, so in this case we might decide that the decision tree model is the
most effective strategy, despite the lower prediction probability. The
Neural Network algorithm generates the second best, the Naïve Bayes algorithm
generates the third best, and the Clustering algorithm generates the worst.
Interestingly, the rank of score for the four models is consistent with the
rank of target population.
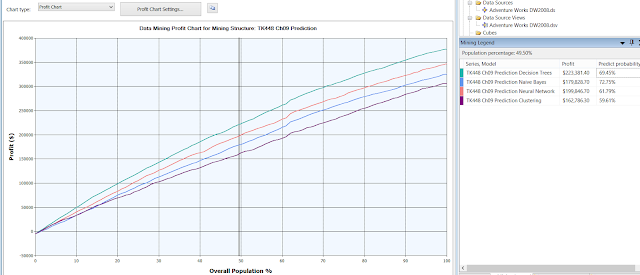
b. Profit Chart
Profit
chart answers the question: what is the correct percent of the population to
target in order to maximize profit? Following is profit chart with four models.
The
figure above is based on the following parameter settings:
|
Setting |
Value |
Comments |
|
Predict value |
1 |
[Bike Buyer] =1, meaning customers who are likely to buy a
bike |
|
Population |
50,000 |
Set
the value for the total target population Your
database might contain many customers, but to save on mailing expenses you might
choose to target only the 50,000 customers who are most likely to respond.
You can get this list by running a prediction query and sorting by the
probability output by the predictive model. |
|
Fixed
cost |
5,000 |
The
one-time cost of setting up a targeted mailing campaign for 50,000 people.
This might include printing, or the cost of setting up an e-mail campaign. We
enter $5,000. |
|
Individual
cost |
3 |
Enter
the per-unit cost for the targeted mailing campaign, $3. This
amount will be multiplied by a number equal to or less than 50,000, depending
on how many customers the model predicts are good prospects. |
|
Revenue
per individual |
15 |
Enter
a value that represents the amount of profit or income that can be expected
from a successful result. In this case, we’ll assume that mailing a catalog
results in purchase of accessories or bikes averaging $15. This
amount will be used to project the total profit associated with high
probability cases. |
It
appears that there are two peak points for the decision tree model on the
chart: one at about 80% (cannot get 80% exactly, I get 79.21% instead) and
another one at about 90%. The results are below:
|
Target population |
Profit |
Predict Probability (Response Rate) |
|
79.21% |
$216,671.30 |
24.78% |
|
90.10% |
$218,025.30 |
15.39% |
Thus,
to maximize profit, we should target 90% of the population. If we do not want
so high percent, we can target 80% of the population, and so on.
As far as how the profit
is calculated, it is unknown to me from the Microsoft sources. But from another
source, I find the profit at the selected population is calculated as:
(True Positive*Revenue) - Fixed Cost -
Action Cost (False Positive + True Positive)
Sometimes
we may need the second form of lift chart, which measures the quality of global
predictions. That is, we are measuring predictions of all states of the target
variable. For example, the chart below measures the quality of predictions for
both states of the Bike Buyer - for both buyers and non-buyers. You can see
that the Decision Trees algorithm predicts correctly in approximately 70
percent of cases, and about 60% for the clustering model (see the legend).
c. Classification Matrices
A
classification matrix shows actual values compared to predicted values. Figure
below shows the classification matrix for the predictive models.
For
the Decision Trees algorithm, for example, we can calculate that the algorithm
predicted 2,575 buyers (741 + 1,834). Of these predictions, 1,834 were correct
(71.2%), while 741 predictions were false, meaning that customers from the test
set did not actually purchase a bike. Of the predicted 2970 (2102+868)
non-buyers, 2102 were correct (70.7%), while 868 predictions were false. The
other three models can be interpreted similarly. Overall, the decision tree
appears to have the largest prediction, followed by Neural Network, then Naïve
Bayes, and finally by clustering.
3. Measuring Reliability - Cross Validation
Figure
below shows the settings for a cross validation and the results of cross
validation of the predictive models.
First,
we define the cross-validation settings as follows:
·
Fold
count - define how many partitions you want to create in your
training data. In Figure below, three partitions are created: when partition 1
is used as the test data, the model is trained on partitions 2 and 3; when
partition 2 is used as the test data, the model is trained on partitions 1 and
3; and when partition 3 is used as the test data, the model is trained on
partitions 1 and 2.
·
Max
cases - define the maximum number of cases to use for cross
validation. Cases are taken randomly from each partition. This example uses
9,000 cases, which means that each partition will hold 3,000 cases.
·
Target
attribute - This is the variable that you are predicting.
·
Target
state - You can check overall predictions if you leave this field
empty or check predictions for a single state that you are specifically
interested in. In this example, you are interested in bike buyers (state 1).
·
Target
threshold - With this parameter, you set the accuracy bar for the
predictions. If prediction probability exceeds your accuracy bar, the
prediction is counted as correct; if not, the prediction is counted as
incorrect.
The full blown
version of the result table is as follows:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The
table above shows that the True Positive classification of Decision Trees does
not give you constant results across partitions. The standard deviation of this
measure is quite high, 95.5. When checking the Neural Network model, you will
see that it is much more constant for the True Positive classification: 15.5,
which means that this model is more robust on different datasets than the
Decision Trees model. From the cross-validation results, it seems that you
should deploy the Neural Network model in production—although the accuracy is slightly
worse than the accuracy of Decision Trees, the reliability is much higher. Of
course, in production, you should perform many additional accuracy and
reliability tests before you decide which model to deploy.